理解并控制数字马达控制系统的量化误差 - 第二部分

作者：Kedar Godbole，德州仪器 C2000 应用产品部

在本文的第一部分中，我们探讨了采样进程及算法实施的量化效应。现在我们提出实验结果以印证第一部分的发现。

下图 1 为系统实施结构图。如前所述，在本文第一部分中，我们采用 16 位定点及 32 位定点 DSP 进行系统实施。

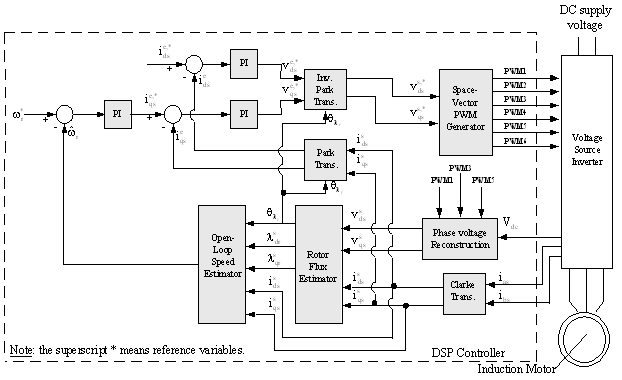
图 1. 马达控制系统的实施

然而，由于定点处理器上的浮点运算是通过运行时间支持库 (rts2800_ml.lib) 实现的，本身效率不高，所以浮点版本的真实实施方式需要较长的采样时间 (4 kHz) 以便计算所有浮点模块。由于不同的采样时间将影响系统性能，所以为了比较方便，实验结果将仅侧重于 16 位与 32 位之间的定点版本。在采样时间不是问题的情况下，浮点与 32 位定点版本的响应是相同的（如第一部分所述）。

比例积分控制器的积分项总是采用 32 位字长甚至是 16 位定点版本，根据以往的经验，采用 16 位积分累加的结果明显地差的多。采用类似仿真的策略将 ±0.5 pu 的步长应用于系统速度参考。d 轴及 q 轴电流和估测速度作为速度命令的步长，这些也证实了仿真结果。在瞬态及稳态状态下，仿真结果的响应相关性很强。不良振荡瞬态及因采用 16 位实施造成的瞬态时间增加等情况下的量化效应是可以验证的。

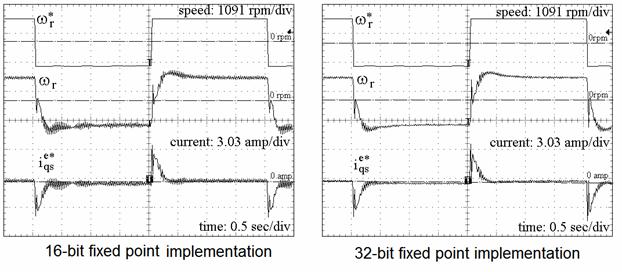
图 2. 实施的估测速度及 q 轴电流

量化及采样频率

要在数字信号处理器的马达控制算法中实现 PID 等控制器，该控制器必须是离散控制器。采样频率的选择是关键的考虑因素，必须遵循能够避免失真的尼奎斯特 (Nyquist) 规定。然而在控制系统中，采样速率几乎总是有必要比尼奎斯特规定建议的大的多。必须在系统 () 较高频率分量时确定采样频率。然后，所选的采样频率 () 必须大于该频率的两倍，即 。仅遵循尼奎斯特规定并不能确保控制系统正常工作。因此，对于一阶系统 (first order system) 而言，通常的做法是选择频率大于 的四倍以上。对于二阶以上的更高阶系统而言，通常选择采样率为较高频率分量的 10 倍。

这样做的目的是为了将内部采样偏移 (inter sample deviation) 控制在可以接受的较小范围内。为说明这种情况，表 1 列出了采样率变化时对控制器系数的影响。在此例中，我们将一个简单的单极点传输函数进行了离散处理。(1) 为传输函数的关系式。

使用以下命令在 Matlab 中进行离散处理：

MATLAB>>SYSD= c2d(tf([100],[1 100]),Ts,’zoh’)

我们可以看到，若采样间隔选择恰当，则系数不会存在明显的问题。但过采样会引起显著的分辨率问题。通过观察该系数的幅度可以了解量化效应。首先是系数分辨率问题。随着采样率的提高，分子系数 (numerator coefficient) 逐渐变小。当采样率为 时，系数下降为 0.00099950016。其 Q15 表示为 0x0020，即 16 位处理器的本机较佳单精度分辨率 (single precision resolution)。这意味着系数分辨率为 5 位，由于系统通常会涉及快、慢动态特性混合并需要复杂的处理过程，所以对16 位处理器来说是个很严重的问题。

其二，分辨率有限可能导致实际控制器会发生“位移”或呈现出与设计模型不同的特性。这些差异可能导致严重的性能问题。对于 16 位处理器而言，要保持高效率就必须具备 16 位系数；多倍精度运算的周期过于密集，留给设计师的系数选择范围对分子而言仅有 4～5 位的分辨率。这些影响都是因为提高采样率引起的。如果系统设计师要提高系统带宽，那么也必须提高采样率。在这种情况下，采用 32 位运算会使数值表示好得多。处理上述情况时，象TI TMS320F2812 数字信号控制器等具有本机 32 位小数表示能力的 32 位处理器可以避免产生上述问题。

数字 PWM 架构及其降频引起的量化问题

嵌入式控制器的数字脉宽调制 (PWM) 架构采用数字计数器与比较寄存器来生成 PWM 输出。高速时钟为计数器提供时钟，计数器的输出计数值与比较寄存器的值作对比。当计数器值超过比较寄存器的值时，PWM 引脚被置为高电平。通过更改比较寄存器的值就可以调制输出。图 3(a) 为概念表示法。

这种方案也有其缺点。PWM 输出的较小变化值等于计数器时钟的时钟周期，当 PWM 频率升高时会产生量化问题。例如，当时钟频率为 50MHz、PWM 频率为 25 kHz 时，PWM 分辨率小于 11 位，不适用于高精度应用。占空比变小时精度降低 2 到 3 位，这与用 300V DC 总线驱动 24V 及 36V 伺服马达的情况相同。当控制功率因数校正级与马达控制反向器相关联时上述情况就显得益发重要。本例中，PWM 频率一般高于 200kHZ，主要是为了降低磁性器件的大小。本例中的 PWM 频率即使达到 100MHz，其分辨率也仅为 8 到 9 位。这可能导致有限周期问题，要解决此问题，则必须更改 PWM 架构。

TI 被称为高分辨率 PWM 的新型架构（首次应用于 TI TMS320F2801、F2806 及 F2808 数字信号控制器）采用全新的调制方法，分辨率为 150 微微秒。该器件转化的相对应的 PWM 分辨率要高的多，几乎消除了数字脉宽调制器的量化影响。

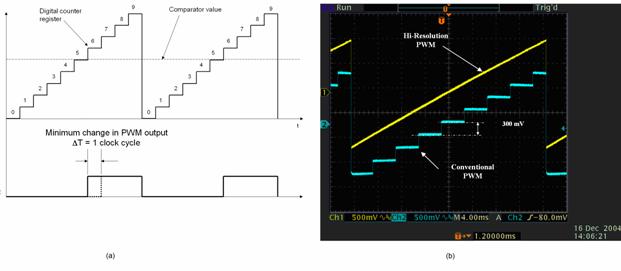
图 3. 标准 PWM 方案图，以及高分辨率 PWM 与传统 PWM 的示波器图比较

图 3(b) 显示了运行中的高分辨率 PWM 及标准 PWM 技术。参考软件图形的斜面，当禁用高分辨率功能时会产生阶梯现象。当启用高分辨率功能时，屏幕上显示了黄色线迹。很容易看出高分辨率 PWM 降低了几个数量级的 PWM 输出量化。对于反向器等 PWM 驱动器件而言，由于 PWM 的时间分辨率简单转换为输出电压分辨率，高分辨率 PWM 产生的增强分辨率有助于降低因有限输出分辨率而导致的有限周期现象的发生。

结论
仿真结果与实验结果的比较显示，16 位系统的性能浮动很大。另一方面，32 位定点系统的性能与浮点系统相同。因为计算的复杂性大为提高会降低系统性能，因此在定点器件上实现浮点算法是不现实的。然而，凭借硅芯片技术的进步以及更小巧的半导体尺寸，我们已于近期推出了超低成本的 32 位定点数字信号处理器，从而系统设计人员能够采用 32 位器件提高马达控制系统的性能。

此外，选用 32 位计算方法不仅使设计人员能够从检查量化细节问题等繁琐的工作中解脱出来，而且还能使用更高的采样率，从而显著提高了对伺服设计人员来说至关重要的系统带宽。为了对量化效应有一个清晰的理解，并使系统性能较优化，解决输出量化问题也很重要。借助高分辨率 PWM 等技术的优势，

相关阅读:

• ...2011/05/27 09:57·理解并控制数字马达控制系统的量化误差 - 第一部分